On a Hierarchy of Algebraic Structures

By Dr. William Pii (Guest writer)

In a recent discussion on a viral arithmetic exercise “6÷2(1+2)”, a question arose regarding some different algebraic structures. I would like to provide a quick reference for some algebraic objects of interest, and consider how they layer upon one another.

To begin, the initial structure, the “zeroth” in a sense, would be mere set with no additional structure. Naively, a set is a collection of elements, essentially a box that may contain some items. More rigorous definitions can be found in a course in mathematical logic and set theory, such as Axiomatic Set Theory by Patrick Suppes. The usual mappings of sets would be functions, which can be defined via sets themselves. Arguably, one could say that modern mathematics is based on sets and functions upon those sets, as one can see in the following structures.

The first structure to impose on a set would be a magma. As defined in Nicolas Bourbaki’s Algebra I, a magma is a pair (M,⋆), where M is a set and ⋆:M×M→M is a binary function. Traditionally, the operation is written with infix notation, where the function symbol appears between the operands, i.e. ⋆(x,y)=:x⋆y. A good example would be the interval M=[0,∞) with the operation x⋆y:=2x+3y. A magma homomorphism from a magma (M,⋆) to (M′,⋆′) would be a function f:M→M′ such that f(x⋆y)=f(x)⋆′f(y) for all x,y∈M.

A more familiar structure would be a semigroup. A semigroup is a magma (S,⋆), where ⋆ is associative, i.e. (x⋆y)⋆z=x⋆(y⋆z). For example, consider any set X with the operation x⋆y:=x. A semigroup homomorphism is simply a magma homomorphism between two semigroups. Clifford and Preston have a multi-volume monograph The Algebraic Theory of Semigroups on the topic.

The next structure introduces an identity element, an element that acts trivially on left or right. Formally, given a semigroup (S,⋆), an identity element is e∈S such that e⋆x=x⋆e=x for all x∈S. Correspondingly, a monoid is a triple (M,⋆,e), where (M,⋆) is a semigroup and e is an identity for (M,⋆). Modifying the previous example, let X be a nonempty set and fix an element e∈X. Define

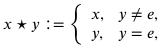
which will be associative like the previous example and forces e to be an identity. A monoid homomorphism is a function f:(M,⋆,e)→(M’,⋆’,e’) such that f(x⋆y)=f(x)⋆′f(y) for all x,y∈M and f(e)=e’, preserving both the operation and the identity. Serge Lang’s graduate text Algebra starts with this structure and builds upward.

At last, a key structure is reached by introducing the notion of an inverse. Given (M,⋆,e) and x∈M, an inverse of x is an element z∈M such that x⋆z=z⋆x=e. If every element of M has an inverse, then (M,⋆,e) is a group. A classical first example would be the symmetries of a regular polygon with composition. Usually, one defines a group homomorphism in the same manner as a semigroup homomorphism, though one can provide that the axioms imply the identity and inverses are also preserved. Most undergraduate and graduate books in abstract algebra, such as Dummit and Foote’s Abstract Algebra, use this structure as a jumping-off point into a full course.

However, the most desired structure in this genre is the abelian group. A group (G,⋆,e) is abelian if the operation ⋆ is commutative, i.e. x⋆y=y⋆x for all x,y∈G. The set of integers under addition is a very important structural example. The maps between abelian groups are merely group homomorphisms.

Now would be a good time to summarize the group axioms and see how the previous structures relate to it. Explicitly, a group is a triple (G,⋆,e), where G is a set, ⋆:G×G→G is a function, and e∈G. These data are subject to the following axioms:

1. ⋆ is associative, i.e. (x⋆y)⋆z=x⋆(y⋆z) for all x,y,z∈G;
2. e is an identity, i.e. e⋆x=x⋆e=x for all x∈G;
3. for all x∈G, there is an inverse of x, i.e. z∈G such that x⋆z=z⋆x=e.

A group is abelian if the following additional axiom is satisfied:

4. ⋆ is commutative, i.e. x⋆y=y⋆x for all x,y∈G.

Notice that monoids, semigroups, and magmas are obtained by merely removing the appropriate axioms from the definition of a group.

Together, these structures form a natural progression from sets to abelian groups, which can be represented by a sequence of categories and forgetful functors below, each merely stripping away an axiom.

At this point, one starts to discuss a set with two binary operations, typically denoted as “+” and “·” to distinguish them. Correspondingly, the structure determined by + is the additive structure, and structure from · is the multiplicative structure.

While weaker structures are discussed, an often used starting point here would be a ring. A ring is a quadruple (R,+,0,·), where R is a set, +,·: R×R→R are functions, and 0∈R such that the following axioms hold:

1. (R,+,0) is an abelian group;
2. (R,·) is a semigroup;
3. · distributes over + on the left, i.e. a·(b+c)=(a·b)+(a·c);
4. · distributes over + on the right, i.e. (b+c)·a=(b·a)+(c·a).

Naturally, Axioms 1 and 2 encapsulate the axioms previously discussed, but will be abridged here for brevity. A good example of a ring would be the continuous real-valued functions on [0,∞) vanishing at ∞. Likewise, a ring homomorphism would be preserve both + and ·. Most abstract algebra texts, including both Lang and Dummit/Foote, discuss rings and higher structures after group theory.

Much like moving from a semigroup to a monoid, a ring can have a multiplicative identity, a unit. Hence, a unital ring is defined as a quintuple (R,+,0,·,1), where (R,+,0,·) is a ring and (R,·,1) is a monoid. An often cited unital ring would be the ring of n×n-matrices over the integers. Of course, a ring homomorphism is unital if it preserves the multiplicative identity.

Parallel to a unital ring would be a commutative ring, where the multiplication is commutative. The most celebrated and important commutative ring would be the integers with conventional addition and multiplication. Homomorphisms between commutative rings are merely ring homomorphisms.

Of special note is a zero ring, where 0=1. This ring is unique up to isomorphism, consisting of a single element, and serves as the terminal object in all three ring categories above. This ring is often regarded as degenerate since it collapses to a singleton, though it serves as a very common ideal and kernel. As such, a common assumption for a unital ring is that 0≠1. This assumption is used often enough that some books include it in the definition of a unital ring.

At the top of this new tower of structures is the field, which is a commutative unital ring such that each nonzero element has a multiplicative inverse. Explicitly, a field would be a quintuple (F,+,0,·,1), where F is a set, +,·:F×F→F are functions, and 0,1∈F satisfying the following field axioms:

1. + is associative;
2. + is commutative;
3. 0 is an identity for +;
4. for each x∈F, there is y∈F such that x+y=y+x=0;
5. · is associative;
6. · is commutative;
7. 1 is an identity for ·;
8. for each x∈F such that x≠0, there is z∈F such that x·z=z·x=1;
9. · distributes over +;
10. 0≠1.

The most common examples of fields would be the rational numbers, real numbers, and the complex numbers with their natural arithmetic. Maps of fields are just unital ring homomorphisms. Notice again that rings, unital rings, and commutative rings can be obtained by omitting or modifying the appropriate axioms.

Mirroring the progression of sets to abelian groups, a similar diagram can be drawn for rings in parallel.

From here, one could add more structure to these algebraic structures, such as topology or order. On the other hand, many graduate texts study actions of groups, rings, and fields upon other structures. These actions give rise to G-sets, R-modules, and F-vector spaces. These topics will be left to a later discussion.

Editor note: 6÷2(1+2) = 9