Yes, Human Chromosome 2 Fusion Really IS Evidence for Common Descent

From: Ration alMind

This is a repost of an article I first wrote up at the end of 2016 on my own blog.

By now I would hope everyone is familiar with the fusion resulting in human chromosome number 2, but for those who aren’t, or would like a quick refresher, here is a short video of Dr Ken Miller explaining it:

Note that that the fusion was a strong prediction of the theory of common descent, in other words, if we didn’t observe the fusion, common descent would be in deep trouble as an idea. This will become important later. Now, putting aside the weak arguments against the fusion itself, the primary way that people opposed to common descent will attempt to reconcile the presence of the fusion is simply to argue that it just proves that humans experienced a chromosomal fusion, not that we share a common ancestor with the other great apes – and they’re absolutely right. An equally plausible scenario to the one that Ken Miller describes in the video above involves humans being specially created as an independent lineage with 48 chromosomes, and then the fusion occurring within that lineage to become fixed so that we all have 46 chromosomes today. Nothing about the fusion necessitates that the human and great ape lineages must be linked.

This was an argument that I wrestled with in my head for a while, until I accepted it and resigned myself to using the fusion as an example of a successful strong prediction of evolution, rather than as some kind of positive evidence for common ancestry. However, a niggling little voice in the back of my mind kept telling me that I was missing something: the fact that common descent requires the fusion while creationism/separate ancestry was ambivalent to it must surely favour common descent somehow. It was only recently, when I learned about Bayes theorem, that I finally found a way to formalise and demonstrate my hunch to be true.

Bayes theorem

Bayes theorem is a remarkably simple equation used to describe the probability of an event by using statistical information related to that event. It was developed by Reverend Thomas Bayes, the famous 18th century English statistician, in a paper entitled “An Essay towards solving a Problem in the Doctrine of Chances” that was published by the Royal Society in 1763, 2 years after his death.

Bayes theorem

In Bayes theorem:

P(H|D) = posterior probability (probability of the hypothesis given the data)

P(D|H) = likelihood (probability of data given the hypothesis)

P(H) = prior probability of the hypothesis

P(D) = prior probability of the data

Don’t be confused by the “prior” and “posterior” probabilities – these just refer to probabilities before and after the data has been taken into account. Simply put, it says that the probability of the hypothesis, given the data, is equal to the probability of the data given the hypothesis, multiplied by the prior probability of the hypothesis, all divided by the prior probability of the data (summed over all hypotheses).

Before we relate this to the chromosome fusion, I’ll run through a quick example to demonstrate how Bayes theorem works:

Imagine that a couple has learned from a sonogram that they’re going to going to have twins, a pair of boys. The doctor tells them that 30% of all twins are identical, while 70% are fraternal (non-identical). What would be the probability that the couple’s twins are identical? This may seem obvious at first – if the probability of twins being identical is 30%, then the probability of the couple’s twins being identical must be 30%, right? Not so fast, there was one more piece of relevant information in the question – we know that the twins are the same sex: they’re both male.

Identical twins must necessarily be the same sex for obvious reasons, while fraternal twins can be either the same sex or different sexes. So, how does the knowledge that both of the couple’s twins are male affect the probability? Let’s run the numbers, plug them into Bayes theorem and see. The hypothesis is that the twins are identical, and the data is that they’re both male.

The prior probability of the hypothesis is simply 0.3 (30%), because 30% of all twins are identical.

The likelihood (the probability of the data if the hypothesis is true) is 0.5 (50%), because if the twins are identical, they must be either both male, or both female. Each of these scenarios is equally likely, so there is a 50% chance that they would both be male.

The prior probability of the data is slightly more complex to calculate. This value is essentially the weighted sum of prior probabilities of the data given all possible hypotheses. The two possible hypotheses are that the twins are identical or that they’re fraternal. If they’re identical, the prior probability that they’re both male will be 0.5, as calculated above, but if they’re fraternal, then the prior probability that they’re both male is only 0.25 (25%), because there are no long just 2 options, there are 4. The twins could both be male, both be female, or one of them be male and the other female, or the other one of them be male and the first one be female. These prior probabilities are then weighted by multiplying them by the prior probabilities of their respective hypotheses:

(0.3*0.5) + (0.7*0.25) = 0.325

So, P(H) = 0.3, P(D|H) = 0.5, and P(D) = 0.325. Using Bayes theorem, we can calculate that the posterior probability (the probability of our hypothesis being correct given our data) is approximately 46%.

So, there is a 46% probability that the couple’s twin boys are identical. This is a classic example of how adding data can affect calculated probabilities – we were able to raise the probability of the couple’s twins being identical from 30% to 46% simply by knowing that they were both boys. Some of you have probably already noticed how the above calculations could be relevant to the fusion and common descent, so without further ado, let’s get apply Bayes theorem to common descent.

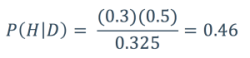
Chromosome 2 and common descent

For the purposes of this post, I’ll just pit common descent against a scenario where humans are an independent lineage from the other great apes, which will be referred to as creationism hereafter. I’ll also assume that prior to the discovery of the fusion, the evidence for common descent and creationism was exactly equal, such that the odds of each one being true was 50-50. This is obviously very generous, but it is necessary for this simple example which only considers the fusion as a piece of evidence in isolation.

In this case, the hypothesis refers to common descent, and the data to the fusion. Let’s plug those terms into our description of Bayes theorem: The probability that common descent is true given that the fusion occurred is equal to the probability of the fusion occurring IF common descent were true, multiplied by the prior probability of common descent being true, all divided by the prior probability of the fusion occurring (summed over all hypotheses: common descent and creationism).

So, remember earlier I said that we were going to assume that ignoring the fusion, the probability of common descent being true was 50%, and the probability of creationism being true being 50%. This gives us the prior probability of our hypothesis (common descent) P(H) = 0.5.

Since the fusion is a strong prediction of common descent, we’ll say that in order for common descent to be true, the fusion MUST have occurred, so this gives us the probability that the fusion would occur IF common descent were true (the likelihood): P(D|H) = 1.

The prior probability of the fusion occurring (P(D)) is equal to the sum of the prior probabilities of each competing hypothesis (common descent and creationism), each multiplied by the probability of the fusion occurring IF that specific hypothesis was correct (the likelihood of that hypothesis). For creationism, we’ve said that the prior probability of that hypothesis being true is 0.5, and let’s say that the probability of the fusion occurring IF creationism was true is also 0.5 (50%), to take into account the fact that creationism doesn’t in any way necessitate the fusion – it’s predictively neutral on the subject. For common descent, we have have already assigned the prior probability (0.5), and the probability that the fusion occurred IF common descent were true (1), so we multiple those numbers together.
To sum it all up: (0.5*1) + (0.5*0.5) = 0.75.
So P(D) = 0.75.

So now we have all the numbers, let’s see what posterior probability we get, and remember that this is the probability of common descent being true given that the fusion occurred.
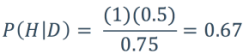
screen-shot-2016-12-30-at-19-26-17

In other words, the probability that common descent is true is 67%, while the probability that it is wrong (and therefore that the alternative hypothesis, creationism, is right) is 33%, given that the fusion occurred.

The key point here is that because creationism doesn’t necessitate the fusion, and is only compatible with it, the probability of observing the fusion IF creationism was true is always going to be less than 1, meaning that P(D) on the denominator of the equation will always be lower than 1 (but still higher than 0.5), ensuring that the posterior probability of common descent being true will always be higher than 50%. This would also work with any other value of P(D|H) that is higher than P(D|H’), where H’ is the creationism hypothesis, so the numbers are quite flexible.

You can verify this for yourself using this calculator. Hypothesis I is common descent, hypothesis II is creationism. Play around with the numbers in the left-hand fields until you’ve convinced yourself that as long as the prior probabilities of the hypotheses are equal (50-50), the hypothesis with the highest likelihood will be favoured. As I’ve explained, the true likelihoods are essentially 100% and 50% for common descent and creationism respectively, but all that’s really required for common descent to be favoured by the fusion is for common descent to “need” the fusion more. At the moment the calculator is set with the numbers we used in the calculation above.

Bottom line

All other things being equal, according to Bayes theorem the chromosomal fusion resulting in chromosome 2 in humans is indeed positive evidence for common descent between humans and the other great apes simply because common descent requires the fusion while creationism does not, even though it might be compatible with the fusion. This is a perfect example of why predictions derived directly from models are so important in science: if your model makes no good predictions and merely accommodates all possible observations, it’s not going to be favoured.

Comments and queries are welcome.

-RM

1 thought on “Yes, Human Chromosome 2 Fusion Really IS Evidence for Common Descent”

Pingback: A Primer on Evolution pt 2: Evidence – Thomas Harper, the Cynical Philosopher